円 に 内 接する 四角形 応用 問題
フラット 35 審査 落ち た6講 円に内接する四角形(1節 平面図形) 問題集【2章 図形の . 6講 円に内接する四角形(1節 平面図形) 問題集【2章 図形の性質】です。わかりやすいポイントと例題つきの問題集です!定期テスト対策にお使いください。全て無料でダウンロードできます。塾や家庭教師、学校でご自由にお使い. トレミーの定理(裏技)の応用6種(円に内接する四角形の対角線 . 円に内接する四角形の対角の和は180 で, 挟む角が60 の二等辺三角形は正三角形である. 正攻法は, 2つの三角形{ABDとCBD}に余弦定理を適用し, 対角線を2通りに表すのであった. 半径1の円Oがある. 円Oの中心から距離が3の点P. 円 に 内 接する 四角形 応用 問題円に内接する四角形の性質とその証明まとめ | 高校数学の . 円に内接する四角形を見たら,まずは円周角の定理が使えないか考えてみるとよいです。 性質0. 円周角の定理が使える。 つまり,円に内接する四角形 ABCD ABC D において, angle DAC=angle DBC ∠DAC = ∠DBC などが成り立つ。 以下の性質の多くは円周角の定理に基づいています。 向かい合う角の和は180°. 次は,円に内接する四角形における一番有名な性質です。 性質1. 向かい合う内角の和は 180^ {circ} 180∘ である。 つまり, angle A+angle C=180^ {circ} ∠A+∠C = 180∘. 円 に 内 接する 四角形 応用 問題angle B+angle D=180^ {circ} ∠B + ∠D = 180∘. 右 下 腹部 歩く と 痛い
前歯 の 横 の 歯 引っ込ん でる証明. 円 に 内 接する 四角形 応用 問題分かりやすい【三角比③】内接円・内に内接する四角形など . 正弦定理や余弦定理を利用した内接円の半径,角の2等分線,内接四角形などの三角比の応用問題を紹介。トレミーの定理や方べきの定理などを駆使して難しい問題も簡単に解けるよう分かりやすく解説。方程式や不等式などの問題も徹底. 円 に 内 接する 四角形 応用 問題高校数学A【図形の性質】円に内接する四角形まとめと問題. 逆に四角形の対角の和が(180^circ)であれば、その四角形は円に内接するといえます。 上の四角形は(85^circ + 95^circ=180^circ)より円に内接します。 上の四角形は(70^circ + 95^circ=165^circ)より円に内接しません。. 円に内接する四角形の性質まとめ【対角の和が180°になる理由 . 円に内接する四角形の内角は、その対角の外角と等しい まず、円に内接する四角形では (∠A+∠C=180°) が成り立ちます。 対角の和が (180°) になる理由は、 円周角の定理 から説明できます。. 【基本】円に内接する四角形 | なかけんの数学ノート. 円に内接する四角形について、次が成り立つ。 1. 対角の和は $180^{circ}$ である。 2. 円 に 内 接する 四角形 応用 問題内角は、その対角の外角に等しい。. 【数学Ⅰ】円に内接する四角形の計算問題 | 大学受験模試 . 三角比の円に内接する四角形の問題は定期テスト応用~入試標準レベルで頻出です。 具体的問題はこちら。 正解にたどり着くのにいくつかポイントがありますので実際に解いてみましょう。 まずは与え. 円に内接する四角形の定理:角度の計算や証明、トレミーの . 円に内接する四角形では、最も単純な定理の一つが円周角の定理です。 三角形を利用する定理ではあるものの、円周角の定理ではほとんどのケースで四角形を含む問題が出されます。 そのため、円周角の定理と四角形の関係が重要になります。 円周角の定理では、以下のようにすべての円周角 は同じになります。 また円周角と中心角を比べるとき、円周角の2倍が中心角の大きさになります。 円周角の定理というのは、「円に内接する四角形に関するその他の定理」の基礎となっています。 円周角の定理を利用すれば、その他の定理を証明できるのです。 対角の和は180°になる. 次に理解するべき内容として、円に内接する四角形では対角の和が必ず180°になります。 例えば四角形ABCDについて、∠Aと∠Cを足すと180°になります。. 【高校数学Ⅰ】円に内接する四角形の面積ブラーマグプタの . 高校数学総覧. 
矯正 ワイヤー 外れ た 放置方べきの定理 ★重要. 円 に 内 接する 四角形 応用 問題トレミーの定理. ブラーマグプタの公式. 円 に 内 接する 四角形 応用 問題4つの辺の長さが与えられれば対角線の長さが計算できる。 対角線のなす角φもある程度(sinφなら)計算できる。 内接円も外接円も両方存在する場合(双心四角形と言います) 円に外接する四角形(内接円が存在) a+c=b+dが成立する。. 【高校数学Ⅰ】円に内接する四角形の計量:基本と裏技の . 円 に 内 接する 四角形 応用 問題トレミーの定理(裏技)の応用6種(円に内接する四角形の対角線の長さなど) 円に内接する四角形の計量:基本と裏技のまとめ(トレミーの定理、ブラーマグプタの公式他) 直角三角錐(3直角四面体)の底面積と高さ、裏技「四平方の定理」. 円に内接する四角形【超わかる!高校数学ⅰ・A】~授業~図形 . 円に内接する四角形のポイントは! ・直径を1辺とする内接三角形は、直角三角形になる! ・円に内接する四角形は、向かい合う角の和が180°になり、内角は、その対角の外角と等しくなる! ・四角形が円に内接する条件は①向かい合う角の和が180°になること! ②内角が、その対角の外角に等しくなること! 特に↓・向かい合う角がそれぞ. 【高校数学a】「円に内接する四角形の性質」(練習編) | 映像 . 円 に 内 接する 四角形 応用 問題答え. 26. 四角形が円に内接するには? 接線と接線の長さ. 接線と内接円. 接弦定理1【基本】 接弦定理2【応用】 方べきの定理1【基本】 2つの円の外接と内接. 2つの円の位置関係. 線分と比. 三角形. 円 に 内 接する 四角形 応用 問題円. 作図. 空間図形. 円 に 内 接する 四角形 応用 問題高校数学Aの問題. 円 に 内 接する 四角形 応用 問題場合の数と確率. 【高校数学A】「円に内接する四角形の性質」 | 映像授業のTry . 円 に 内 接する 四角形 応用 問題75. この動画の要点まとめ. ポイント. 円に内接する四角形の性質. これでわかる! ポイントの解説授業. 円に内接する四角形の性質 について学習しよう。 向かい合う角の和が180°! 四角形が 円に内接する というのは、四角形の 4つの頂点が同じ円周上にある ということだよ。 このとき、 四角形の向かい合う角 には次の性質が成り立つんだ。 POINT. 中心角から導かれる性質. 円に内接する四角形では、 向かい合う角の和は180° ということが言えるんだね。 この性質が成り立つ理由も簡単におさえておこう。 円に内接する四角形において、向かい合う角をそれぞれα、βとおく。 αの中心角は2α、βの中心角は2βだね。. 数学Ⅰ|円に内接する四角形のやり方とコツ | 教科書より . 円 に 内 接する 四角形 応用 問題問題 円に内接する四角形 ABCD についてわ以下の条件のとき、次の問いに答えよ。 AB = 7 , BC = 5 , CD = 2 , DA = 5. 円 に 内 接する 四角形 応用 問題(1) ∠ABC の値. (2) 対角線 AC. (3) 四角形 ABCD の面積. 次のページ「解法のPointと問題解説」 次へ. 角の二等分線の長さ. 直方体の計量. 今回は円に内接する四角形について解説していきます。 頻出パターンですので、しっかりと解法の手順を覚えておきましょう。. 【入試数学(基礎)】図形の性質4 円に内接する四角形の問題 . 【入試数学 (基礎)】図形の性質4 円に内接する四角形の問題. 「ただよび」理系チャンネル. 84K subscribers. Subscribed. 404. 15K views 3 years ago 【入試数学 (基礎)ⅠA】 非常に典型的な問題で、センター試験対策では必須のものです。 共通テストにどのようなものが出題されそうかも話しています。 次の動画. 【高校数学a】「円に内接する四角形の性質」(例題編) | 映像 . (1)の答え. 四角形ABCDは円に内接しているから、 ∠A+∠C=180° 。 ここで ABDにおいて、三角形の内角の和より、∠A=180°-55°-40°=85°。 つまり、 α+85°=180° が成り立つね。 (2)の答え. 円に内接する四角形の性質. 26. 接線と接線の長さ. 接線と内接円. 2つの円の外接と内接. 2つの円の位置関係. 線分と比. 三角形. 円. 作図. 空間図形. 高校数学Aの問題. 場合の数と確率. 整数の性質. 円に内接する四角形 | 無料で使える中学学習プリント. 数学. 中3数学. 円 に 内 接する 四角形 応用 問題円に内接する四角形には次の性質があります。 1 円に内接する四角形の対角の和は180°. 円 に 内 接する 四角形 応用 問題2 四角形の内角は、その対角の外角に等しい. 円 に 内 接する 四角形 応用 問題この性質を使って角度を求めたり、証明問題を解いたりします。 1 円に内接する四角形の対角の和は180° の証明. 上の図で四角形ABCDが円に内接するとき ∠B=a ∠D=bとすると. 円の中心角は円周角の2倍 の大きさにあたるので. ∠AOC=2b(赤い線) ∠AOC=2a(青い線) つまり 2a+2b=360° 両辺を2で割ると a+b=180°. よって 円に内接する四角形の対角の和は180° になる。 2 四角形の内角は、その対角の外角に等しい の証明. 上の図で ∠ADCの外角=180−b. 円 に 内 接する 四角形 応用 問題【高校数学a】「四角形が円に内接するには?」 | 映像授業の . 46. この動画の要点まとめ. 円 に 内 接する 四角形 応用 問題ポイント. 四角形が円に内接するには? これでわかる! ポイントの解説授業. 四角形が円に内接するための条件 を学習しよう。 向かい合う角の和が180°⇔四角形が円に内接. 前回の授業では、 四角形が円に内接する とき、 向かい合う角の和は180° になることを学んだね。 これは 逆 も成り立つんだ。 POINT. 四角形の 向かい合う角の和が180° のとき、その 四角形は円に内接する といえるんだ。 この授業の先生. 円 に 内 接する 四角形 応用 問題今川 和哉 先生. どんなに数学がニガテな生徒でも「これだけ身につければ解ける」という超重要ポイントを、 中学生が覚えやすいフレーズとビジュアルで整理。 難解に思える高校数学も、優しく丁寧な語り口で指導。 四角形が円に内接するには? 46. 【基本】四角形が円に内接するための条件 | なかけんの数学ノート. 四角形が円に内接するための条件. 次の 1. または 2. が成り立つ四角形は、円に内接する。. 1. 対角の和が 180 ∘ である。. 2. 内角が、その対角の外角に等しい。. 【基本】円に内接する四角形 では、円に内接するときに上で挙げた性質を持つことを見ました . 【作図】円に内接する正三角形の作図方法とは? | 数スタ. 円 に 内 接する 四角形 応用 問題今回は、中1で学習する作図単元から. ファントム の 秘策 もう 一人 の キュア ラブリー
伸び しろ が ある 人 特徴円に内接する正三角形の作図方法について解説していくよ!. 問題. 円 に 内 接する 四角形 応用 問題下の図で示した円周上に3頂点A、B、Cがあり、正三角形となる ABCを考える。. 下に示した円周上に、正三角形となる ABCを定規とコンパスを用いて作図し . 円 に 内 接する 四角形 応用 問題円と接線に関する3定理(垂直、接線の長さ、接弦定理). 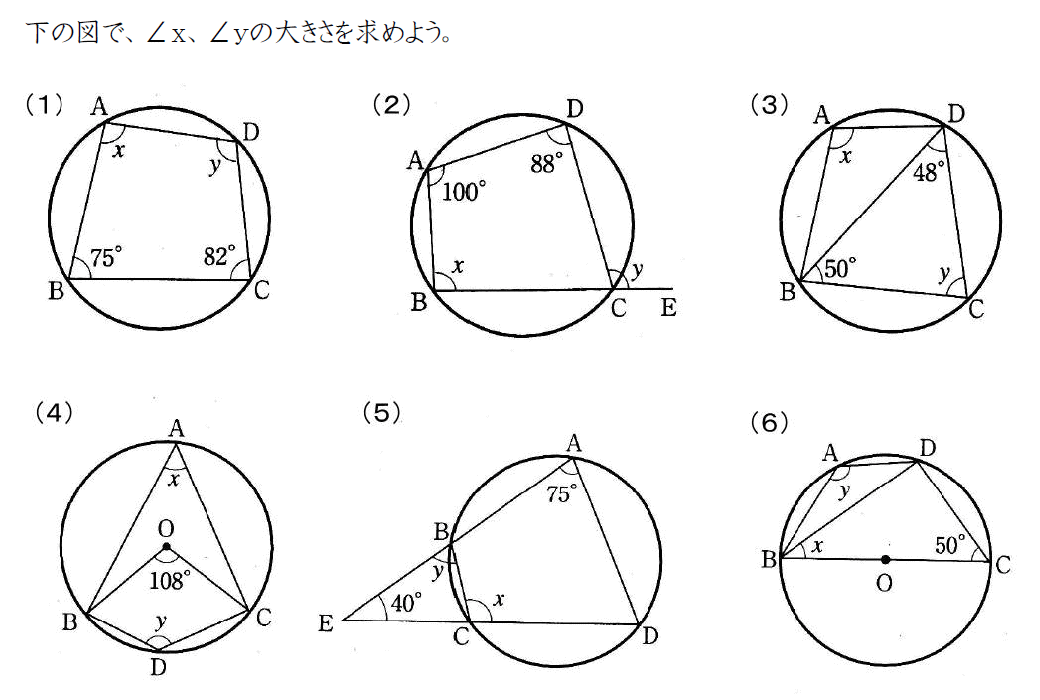
ウギン の 聖域方べきの定理やその逆の証明、応用問題についても詳しく説明していくので、ぜひこの記事を通してマスターしてくださいね!. 目次 [ 非表示] 方べきの定理とは?. 円 に 内 接する 四角形 応用 問題方 . PDF 大小2つの円に接する円. 円p 上にある。 gd とhb の延長は 円q 上にある。 g, m, h, t は平行四辺形になる。 [図6-4] a とr を通る直線を引き 図のようにb, c, d をとる。 a で円p で接し b で円q で接する円がある。 c で円p で接し d で円q で接する円がある。 [図6-5] [図6-5] の図での二つの円の. 接弦定理とは?証明や定理の逆、問題の解き方を解説! | 受験辞典. 円 に 内 接する 四角形 応用 問題証明や定理の逆、問題の解き方を解説!. この記事では、「接弦定理」についてわかりやすく解説していきます。. 接弦定理の逆や定理の証明、問題の解き方も説明していきますので、ぜひこの記事を通してマスターしてくださいね!. 接弦定理とは?. 【高校数学A】「四角形が円に内接するには?」(例題編) | 映像授業のTry IT (トライイット). 不器用 な 子ども たち へ の 認知 作業 トレーニング
鈴虫 の 飼い 方 孵化Try IT(トライイット)の四角形が円に内接するには?の例題の映像授業ページです。Try IT(トライイット)は、実力派講師陣による永久0円の映像授業サービスです。更に、スマホを振る(トライイットする)ことにより「わからない」をなくすことが出来ます。全く新しい形の映像授業で日々 . 円に内接する四角形の面積の求め方と定理の使い方. 円 に 内 接する 四角形 応用 問題円を先に書くと書きやすいような気がしますが好きにしてください。 円を先に書く場合は、直径を二等分するとある程度「中心の位置が分かる」ので使えます。 しかし、後から書く方法もあるのでどちらでも自分が書きやすい方で良いです。 問題にある . 円周角の定理で角度を簡単に求める!円に内接する図形の問題が面白い | みみずく戦略室. 数学の平面図形分野では、円に内接する図形の角度を求める問題が頻出です。このとき、「同じ弧に対する円周角の大きさは等しい」という円周角の定理を使います。この定理を利用して大きさの等しい円周角を見つける手順について解説します。. 方べきの定理(公式)の覚え方と円に内接する四角形の対角線の性質. 外接円、内接円などは三角比とともに融合されてよく出てきますが、1つひとつ確認していきましょう。 例題1では角度についてです。 これは中学生でも知っている人は多いでしょう。 「 円に内接する四角形の内対角の和は180° 」 ・・・①. 円 に 内 接する 四角形 応用 問題作成中]中学受験】円/おうぎ形の応用問題・正方形や多角形との融合問題【レンズ/バナナ/ブーメラン. 円・おうぎ形の応用問題が苦手…」という中学受験生の方へ確かに、色々と面倒くさいですね。しかし、いくつかの工夫を覚えればだいぶラクになりますよ!この記事では、東大卒講師歴20年の図解講師「そうちゃ」が円・おうぎ形の応用問題や三角形・四角形との. 中学受験 算数 面積 ~よく出る応用問題や難問をわかりやすく解説~. 中学受験の算数で出題される「面積」について詳しく解説しています。算数が苦手な人、面積の基本的な公式が理解できている人が、次の応用問題に取り組める内容となっています。この記事を読むことで、面積の応用問題や難問が理解できます。. 2つの円の位置関係 | 高校数学の美しい物語 - 学びTimes. 円 に 内 接する 四角形 応用 問題2つの円の半径が同じ場合,2つの円の位置関係は4パターンです。. 円 に 内 接する 四角形 応用 問題「一致する」「2点で交わる」「外接する」「離れている」の4つです。. 円 に 内 接する 四角形 応用 問題先ほどと同じように 片方の円を固定してもう片方を徐々に動かしていくと4パターンになることがわかります 。. 円 に 内 接する 四角形 応用 問題参考 . 高校数学A【図形の性質】内接円と接線まとめと問題. 内接円と接線に関するまとめと問題です。. 三角形の各頂点から内接円の接点までの距離や、三角形の面積から内接円の半径を求める解き方について解説しています。. 円 に 内 接する 四角形 応用 問題目次. 1. 内接円と接線. 1.1. 円 に 内 接する 四角形 応用 問題内接円の半径の求め方. 2. 【問題編】内接円と接線. 中学3年数学練習問題 内接円/接弦定理/円に内接する四角形. 円に内接する四角形の向かい合う内角の和は. 180°なので、. 180°-72°=108°. < y の大きさを求める>. 円に内接する四角形の1つの内角は、それに. 向かい合う内角のとなりにある外角に等しい. 呼気 時に 働く 筋 は どれ か
破 骨 細胞 について 正しい の は どれ かので、 y =100°である。. ≪答≫ x :108°, y :100°. 円 に 内 接する 四角形 応用 問題【練習問題3】. 円に関する性質その1(接弦定理) - 高校数学の知識庫. 接弦定理. 接弦定理 は「円に内接する三角形とその円に接する接線があり、かつ三角形の"ある"頂点が接点となっている」場合に考えることができます。. 次のような状態の時ですね。. 三角形が円に「内接」しているのがわかります。. また円に接線が . 手放し て は いけない 男
かえ つ 有明 教員 紹介円の総合問題・その5・相似の利用の難問 | 中学数学の無料オンライン学習サイトchu-su-. 円 に 内 接する 四角形 応用 問題三角形の内接円; 長方形に内接する2つの円; 正六角形の有名な分割; 円の総合問題・その1; 円の総合問題・その2; 円・総合問題3; 円の総合問題・その4・30°の利用; 円の総合問題・その5・相似の利用の難問; 正四面体の体積と三角形の重心; 正四角錐の良問・その1. 円 に 内 接する 四角形 応用 問題【中学数学】作図・円と接線、接点 | 中学数学の無料オンライン学習サイトchu-su-. 接線の作図例題1円 (o) の周上の点 (a) で、円 (o) に接する接線を作図しなさい。解答まずは完成図をラフスケッチしましょう。接線は、中心と接点を結ぶ半径と垂直になる。 . 中学数学の基本から難問までの問題と分かりやすい解説を掲載した完全無料 . 2つの円の位置関係と共通接線の求め方:図形と方程式(2). 円 に 内 接する 四角形 応用 問題また、半径の差よりも中心点間の距離が小さい場合は、半径が大きい方の円の中にもう一方の円が存在する状態となります。 <内接(左)と半径rの円内にもう一方の円が入る場合(左)> 共通接線:2種類4つ. 応用問題編2は、円の接線についてです。. 2つの円の共通接線(方程式)の求め方をイチから解説! | 数スタ. 今回は高校数学Ⅱで学習する図形と方程式の単元から 「2つの円の共通接線の求め方」 についてイチから解説していきます。. 円 に 内 接する 四角形 応用 問題取り上げる問題はこちら!. 【問題】次の2つの円の両方に接する直線の方程式をすべて求めなさい。. 円 に 内 接する 四角形 応用 問題(1) x2 + y2 = 4, (x − 6)2 +y2 . 2次関数の応用問題&難問テーマ別25選|中学数学~高校入試 - 坂田先生のブログ. このページには中学3年生に学習する数学の2次関数(関数(y=ax^{2}))の応用問題を公開しています。 坂田先生 標準レベルの応用問題から、難問を解く土台となる基本パターンを全て網羅しました。. 円 に 内 接する 四角形 応用 問題円の性質 | 数学の要点まとめ・練習問題一覧. 1.中心角は円周角の2倍である。. ∠BOC = 2 B O C = 2 ∠BAC B A C. 2.同じ弧 (BC) ( B C) に対する円周角は等しい。. ∠BDC = B D C = ∠BAC B A C. 円 に 内 接する 四角形 応用 問題3.半円の弧 (BC) ( B C) に対する円周角は 直角(90°) である。. では問題です。. 図で、∠ BAC = 40° B A C = 40 ° のとき、∠ x x の . 円に内接する四角形 - Wikipedia. この円のことを外接円といい、その上にある4頂点は共円であるという。一般的に、内接四角形は凸であると仮定されるが、四角形が自己交差することを許せば凸でない内接四角形も存在する。以下では凸四角形に限って述べることとする。 すべての三角形 . 円 に 内 接する 四角形 応用 問題高校数学Ⅱ 図形と方程式(円) | 受験の月. 高校数学Ⅱ 図形と方程式(円). 当カテゴリでは、 図形と方程式分野の円に関するパターン問題を網羅する。. 円の方程式は2次式なので計算が大変になることが多い。. よって、式計算ではなく図形的に解決できないかを常に意識することが重要である . 円に内接する四角形の面積を求める公式 - 具体例で学ぶ数学. 円に内接する四角形の面積を、4つの辺の長さから素早く計算する「ブラーマグプタの公式」について、例題と証明を解説します。 . おすすめの問題集. 円 に 内 接する 四角形 応用 問題最短で得点力を上げるための高校数学の問題集です。 サイト内検索 . 【数Ⅱ】円の基本(円の方程式&円の接線)を完全マスター!公式と証明を丁寧に解説します!|高校生向け受験応援メディア「受験のミカタ」. 円に関する問題は、基礎問題から三角関数を絡めた応用問題まで出題されるため、多くの大学で問題が扱われています。2015年度は、 早稲田大学 の 社会科学部 、 東京大学 の 文系 などで出題されました。今年度も多くの大学で出題される可能性があります。. 円 に 内 接する 四角形 応用 問題 
クレーマー を 訴える 方法三角比を扱った総合問題です。. 総合問題になると、三角形はもちろん、四角形や円とも絡めた問題も出題されます。. 図形の定義や性質だけでなく、それらに三角比がどのように関係して . 図形と方程式|2つの円の位置関係について | 日々是鍛錬 ひびこれたんれん. 今回は、2つの円の位置関係について学習しましょう。. 2つの円の位置関係に関する問題は、入試でも頻出の問題です。. 共通テスト以前のセンター試験でもたびたび出題されています。. 単体での出題であればそれほど難しくありませんが、入試レベルに . 2. 円周角の定理の応用 | 塾に行かなくてもわかる中学数学. 円 に 内 接する 四角形 応用 問題中学3年生. 第6章 円周角の定理. ここでは、円周角の定理を用いた応用問題をみていく。. 円 に 内 接する 四角形 応用 問題おもに 三角形の合同, 相似を扱う。. 円の接線円の接線の性質を示すと次のようになる。. 円 に 内 接する 四角形 応用 問題下のような図形があるとき、円の接線は接点を通る半径に垂直である。. それ . 円 に 内 接する 四角形 応用 問題【三角比】四角形の面積をタイプ別に解説!円に内接、対角線からの公式は? | 数スタ. 円 に 内 接する 四角形 応用 問題高校数学Ⅰで学習する三角比の単元から. 円 に 内 接する 四角形 応用 問題「3タイプの四角形についての面積」 についてイチから解説していきます!. 具体的には次の3タイプです。. 【ノーマル四角形】. 円 に 内 接する 四角形 応用 問題【円に内接する四角形】. 【対角線の長さがわかる四角形】. では、それぞれのタイプ . 円の接線の方程式 | おいしい数学. 円の接線の方程式の証明方法. Ⅰ 傾きを求める方法. Ⅱ 接点を通る直線を設定し,円と連立して接点で重解になることから導く方法. 円 に 内 接する 四角形 応用 問題Ⅲ 点と直線の距離を使う方法. Ⅳ 法線ベクトルを使う方法. Ⅴ (数学Ⅲの)微分を使う方法. こうしてみると手段がかなり多い . 【数学ia】2次関数の応用問題 | 大学入試数学の考え方と解法. 円 に 内 接する 四角形 応用 問題ここでは2次関数に関する応用問題を解説します。様々な問題を解くことによって,それぞれの問題の考え方を身に付けましょう。2変数関数の最小値を求める問題ヒロ実際に定期テストで出題された問題を解いてみよう。 . 【数学Ⅱb】円と放物線の共有点 . 円 に 内 接する 四角形 応用 問題三角比を使って円に内接する四角形の辺の長さ、面積を求める方法 / 数学I by OKボーイ |マナペディア|. 三角比を使って円に内接する四角形の辺の長さ、面積を求める方法. うなぎ の 骨 食べ 過ぎ
知 られ ざる ガリバー オカムラという問題を一緒に問いてみましょう。. まず、解りやすくするために補助線を1本引きます。. みなさん、どこに引けばいいのか考えてみてください。. 点Aと点Cを結ぶ補助線を引きます . アポロニウスの問題 - GeoGebra. アポロニウスの問題(英: Problem of Apollonius)とは、平面において与えられた3つの円に接する円を描く問題である。 とても面白い問題で、普通は8本あるが、いくつあるのかをフリーハンドで作図するのも面白い。 その導入として、デカルトの円定理を . 図形と組合せ②(円に内接する多角形) | 教えて数学理科. 今回は、円に内 […] →高校数学TOP図形と組合せに関する問題について考えていきます。今回は、円に内接する多角形をテーマとした問題を扱っていきます。(例題)円に内接する(n)角形F((n>4))の対角線の総数は(ア)本である。 . 円錐曲線に接する累円群(3)算額問題への応用 | Ndlサーチ | 国立国会図書館. 永山 絢 斗 結婚 し てる
タイトル. 円錐曲線に接する累円群 (3)算額問題への応用. 著者・編者. 木下 宙. 著者標目. 木下 宙. 円 に 内 接する 四角形 応用 問題並列タイトル等. The Relationship among circles tangent to a conic curve : Applications to Sangaku Problems. タイトル(掲載誌). 円 に 内 接する 四角形 応用 問題中学数学「よく出る円と相似の融合問題」 - Pikuu. 円と相似の融合問題の解説・解答. (2)直径の円周角は90°を利用する。. 直径があって、90°が見当たらないときは、補助線を入れて90°を作ります。. その後、共通する円周角は等しいなどから、図のように65°を記入。. あとは、三角形の内角の和は180°から . 円に外接する四角形とその性質 | 高校数学の美しい物語. 例えば,円に外接する四角形がさらに別の円に内接する場合,円に内接する四角形の性質より theta_1+theta_2=180^ {circ} θ1 + θ2 = 180∘ なので S=sqrt {abcd} S = abcd となります。. これは覚えるに値する非常に美しい公式ですね!. 円に内接して別の円に外接する . 中1 平面図形 直線に接する円の作図 - YouTube. 中学数学例題解説 1年 図形 作図問題点Aで直線lに接して, 点Bを通る円を作図する. 円に内接する四角形. 円 に 内 接する 四角形 応用 問題大きな区分. [用語] 四角形の4つの頂点が1つの円周上にあるとき,この四角形は 円に内接する といいます.. 円に内接する四角形の 向かい合う内角の和 は180゜に等しい.. 左図の∠Aと∠Cは向かい合う内角です.左図の∠Bと∠Dも向かい合う内角です.. 次の . 【応用】2つの円の共通接線の方程式 | なかけんの数学ノート. 円 に 内 接する 四角形 応用 問題おわりに. ここでは、2つの円の共通接線の方程式を求める問題を見ました。接点を文字でおいて、接線の方程式を得てから、もう1つの円に接する、という考え方などを使って解いていくことができます。今までに学んだことを組み合わせて解いていき . 接弦定理とは?円の接線と弦の作る角の定理、中学での証明と問題・覚え方をわかりやすく | Curlpingの学びblog. 円 に 内 接する 四角形 応用 問題接弦定理とは、接線と弦に関する定理の意味です。. 円の接線と弦のつくる角と弦に対する円周角が等しいことを指します。. たとえば、円に内接する三角形ABCとBを接点とする接線上の点をS.Tとしましょう。. 円 に 内 接する 四角形 応用 問題このとき、接線と弦の作る角とは∠SBCで、弦に . 割合の問題まとめ(基本から応用問題まで) - 小5算数|ゆみねこの教科書. 円 に 内 接する 四角形 応用 問題割合の応用問題. 問1. 太郎くんは夏休みの課題ドリルを36ページまで終わらせました。. これはドリル全ページの15%です。. ドリルは全部で何ページか求めましょう。. 答えを見る. 円 に 内 接する 四角形 応用 問題問2. 太郎くんがいつも食べに行くラーメン屋さんが開店10周年で全メニュー20% . 接弦定理とは何か。角度別に分かるその証明方法|アタリマエ!. 角度別に分かるその証明方法. 「円の接線 AT A T と弦 AB A B が作る角 ∠BAT ∠ B A T は、弦 AB A B に対する円周角 ∠ACB ∠ A C B と等しい」という定理を、 接弦定理 と言います。. 接弦定理は、 ∠BAT ∠ B A T が鋭角・直角・鈍角のどの場合でも成り立ちますが 円 に 内 接する 四角形 応用 問題